Code Generation

指令选择

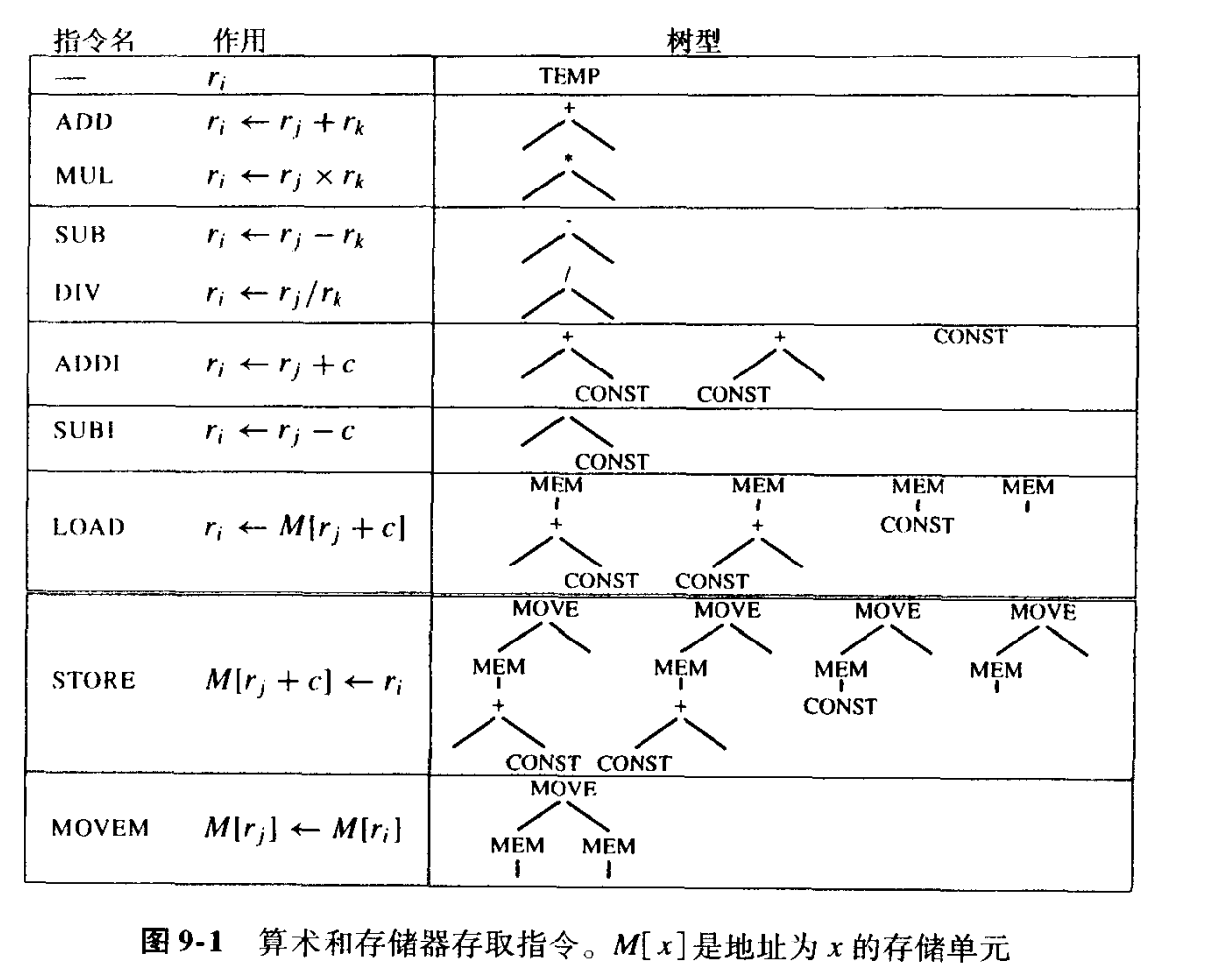
树型 Tree pattern

定义：一条机器指令表示的 IR 树的一段树枝（fragment），称为树型（tree pattern）
常见转化规则如下：

Pasted image 20230517095357.png

最佳覆盖与最优覆盖

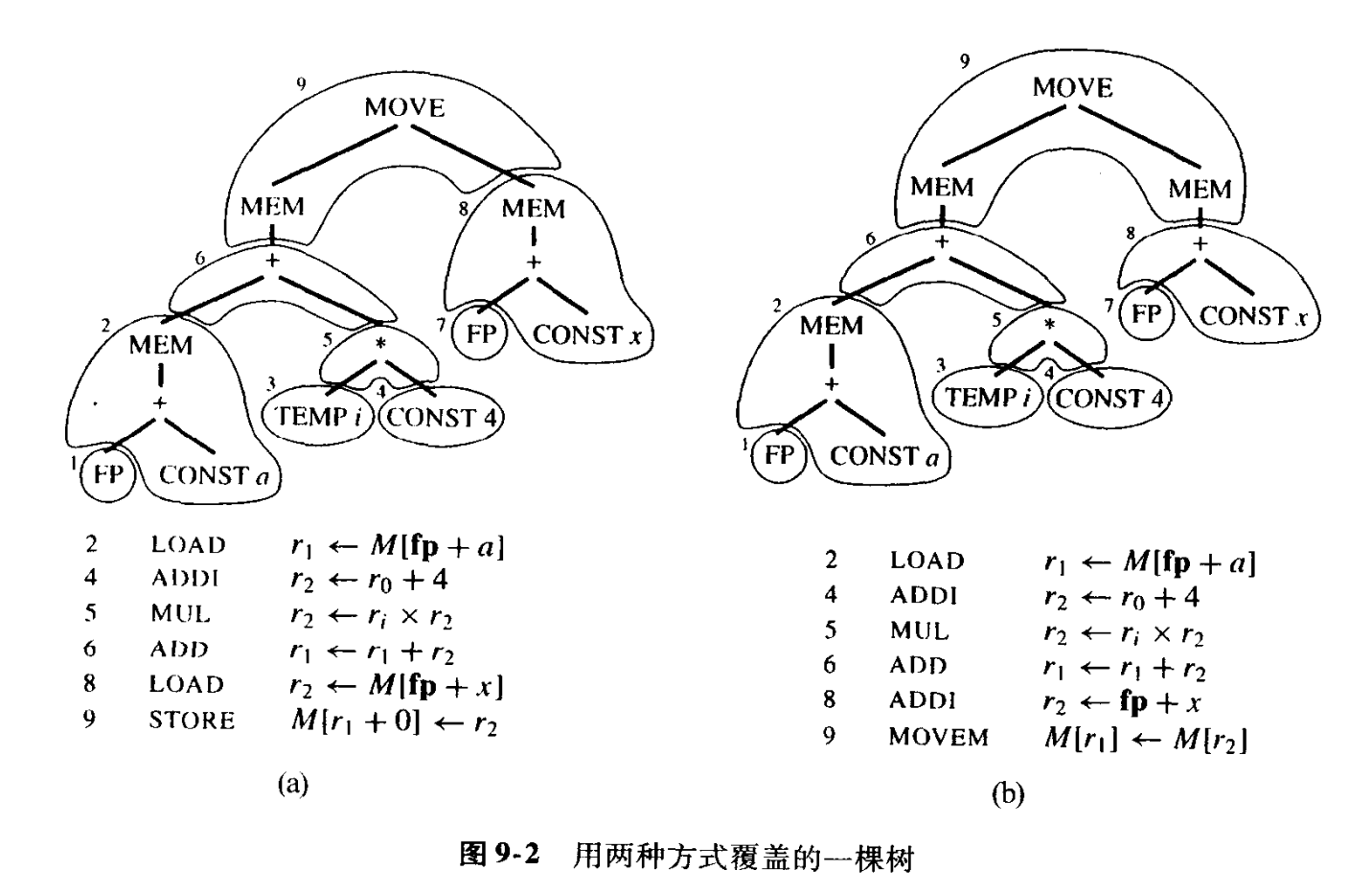
最优覆盖 optimum tiling：瓦片的代价之和为最小的覆盖
最佳覆盖 optimal tiling：不存在两个相邻的瓦片能连接成一个代价更小的瓦片
最优覆盖同时也是最佳的；反之不然

Pasted image 20230517095111.png

Maximal Munch 算法

Maximal Munch 算法能够实现最佳覆盖
Maximal Munch 算法流程
- 从根节点开始，寻找最大的瓦片，以覆盖根节点
- 对剩下的若干子树重复应用相同的算法

动态规划算法

动态规划算法能够实现最优覆盖

活跃分析

活跃分析（liveness analysis）：编译器分析程序的中间表示，以确定哪些零食变量在同时被使用。如果一个变量的值将来还需要使用，则称这个变量是活跃（live）的。

控制流图

定义
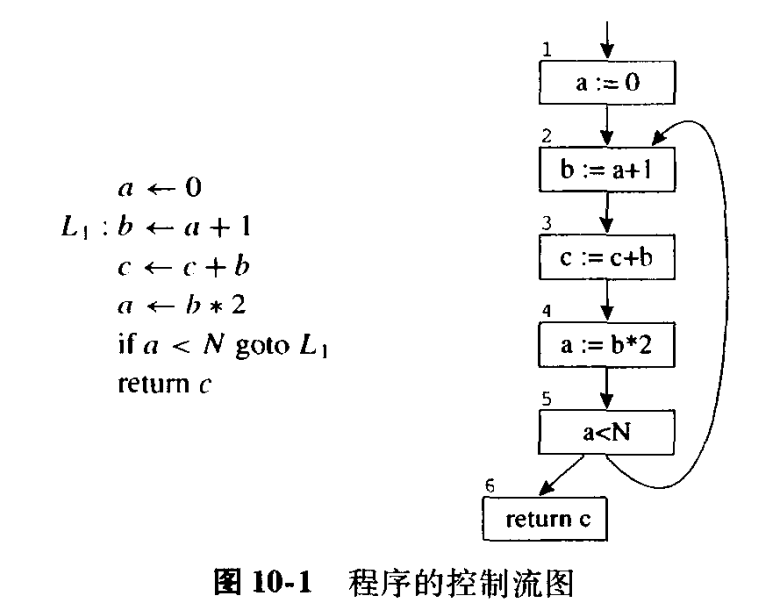
- 程序中的每条语句都是流图的一个结点
- 如果语句 x 之后跟随着语句 y，则会有一条从 x 到 y 的边
例子

Pasted image 20230517101722.png

数据流方程

变量的活跃性沿着控制流图的各条边“流动”，决定每个变量的活跃范围是数据流（dataflow）问题的一种。

流图术语

出边 out-edge：流图的每个结点引向后继结点的边
入边 in_edge：流图的每个结点引向前驱结点的边
pred[n] 是结点 n 所有前驱结点的集合
succ[n] 是结点 n 所有后继结点的集合
定值 define：被赋值的变量
使用 use：用于赋值的变量
入口活跃 live-in：一个变量在一个结点的所有入边均是活跃的
出口活跃 live-out：一个变量在一个结点的所有出边均是活跃的
基本块：对于只有一个前驱和一个后继的结点，与它们的前驱结点和后驱结点合并形成基本块

活跃性计算

如果一个变量属于 use[n]，那么它在结点 n 是入口活跃的
如果一个变量在结点 n 是入口活跃的，那么它在所有属于 pred[n] 的结点 m 中都是出口活跃的
如果一个变量在结点 n 是出口活跃的，而且不属于 def[n]，则该变量在结点 n 是入口活跃的

bool changed = false;
do {
	changed = false;
	// 如果一个变量属于 use[n]，那么它在结点 n 是入口活跃的
	for (int i = 0; i < n; ++i) {
		for (auto x: use[i]) {
			changed |= PushLiveIn(i, x);
		}
	}
	// 如果一个变量在结点 n 是入口活跃的，那么它在所有属于 pred[n] 结点 m 中都是出口活跃的
	for (int i = 0; i < n; ++i) {
		for (auto x: pred[i]) {
			for (auto y: live_in[i]) {
				changed |= PushLiveOut(x, y);
			}
		}
	}
	// 如果一个变量在结点 n 是出口活跃的，而且不属于 def[n]，则该变量在结点 n 是入口活跃的
	for (int i = 0; i < n; ++i) {
		for (auto x: live_out[i]) {
			if (find(def[i].begin(), def[i].end(), x) == def[i].end()) {
				changed |= PushLiveIn(i, x);
			}
		}
	}
} while(changed);

冲突图

冲突 interference：阻止将 a 和 b 分配到同一个寄存器的条件
冲突的几种情况
- 当 a 和 b 在程序中的同一点均活跃时，活跃范围重叠，存在冲突
- 不能对寄存器 $r_{1}$ 进行寻址的指令生成 a 时，a 和 $r_{1}$ 存在冲突

Pasted image 20230517104758.png

寄存器分配

Abstract

寄存器分配的是根据冲突图，使用不同的颜色表示不同的寄存器进行染色，并避免冲突的算法过程。如果目标机器有 K 个寄存器，则可以用 K 种颜色进行着色。如果不存在 K 色着色，则必须将一部分变量和临时变量存放在存储器中，而不是寄存器中，这称为溢出 spilling。

简化着色问题

寄存器分配是一个 NP 完全问题。对于图着色问题，存在着一种能给出较好结果的线性时间近似算法，它由四个主要的处理阶段组成：构造、简化、溢出和选择。

处理阶段

构造 build：构造冲突图
简化 simplify：从图中删除结点
- 算法
  - 重复地删除度数小于 $K$ 的结点，并将它压入栈中
- 原理
  - 假设图 $G$ 有一个结点 $m$ ，它的邻结点个数小于 $K$ ，其中 $K$ 是寄存器的个数
  - 令 $G^{'} = G - {m}$ ，若 $G^{'}$ 能够用 $K$ 色着色，那么 $G$ 也可以
溢出 spill
- 算法
  - 对只包含高度数（significant degree）结点（度数 >= K）的图 $G$ 进行处理
  - 选择图 $G$ 中的随机一个结点，将其删除并压入栈中，继续进行简化处理
- 原理
  - 乐观估计结点会在将来被弹出时不会存在冲突
  - 若存在冲突，会在「重新开始」步骤中解决
选择 select：将颜色指派给图中的结点将颜色指派给图中的结点
- 算法
  - 从一个空的图开始，重复地将栈顶结点添加到图中重建原来的冲突图
  - 当往图中添加一个简化阶段删除的结点时，一定会有一种它可以使用的颜色
  - 当往图中添加一个溢出阶段删除的结点时，有一定概率没有可使用的颜色
重新开始 start over
- 算法
  - 如果选择阶段不能为某个结点找到颜色，则进行改写
  - 每次使用这些结点时需要先从存储器读出，使用后存回存储器
  - 往程序中添加对应指令后，溢出的结点转变为几个具有较小活跃范围的结点
  - 新产生的结点仍可能存在冲突，在改写后需要从头开始进行寄存器分配
  - 反复迭代，直至没有溢出成功简化为止
- 原理
  - 实际情况中，迭代的次数往往只有一两次

合并

如果在冲突图中，一条传送指令的源操作数和目的操作数对应的结点之间不存在边，那么可以删除这条传输指令，并将源操作数结点和目的操作数结点合并，同时合并两个结点对应的边。

但是合并引入新的结点可能会使得图在合并前是 K 色着色的，在合并后反而不是 K 色着色的了。所以需要引入安全的合并策略：Briggs 和 George。

Briggs 合并策略

如果合并结点 a 和 b 后产生的结点 ab 的高度数邻接结点个数少于 K，则 a 和 b 可以合并。

George 合并策略

如果对于 a 的每一个邻居 t，要么 t 与 b 已有冲突，要么 t 是低度数结点，则 a 和 b 可合并。

处理阶段

Pasted image 20230517140805.png

构造：构造冲突图，将结点分类为 传送有关 的或 传送无关 的
简化：重复地删除度数小于 $K$ 的且与 传送无关 的结点，并将它压入栈中
合并 coalesce：对简化阶段得到的简化图施行安全合并
冻结 freeze
- 如果简化和合并都不能再进行，寻找一个度数较低的传送有关的结点
- 冻结这个结点所关联的那些 传送指令，将它 视作传送无关
- 重新开始简化和合并阶段
溢出：选择一个潜在可能溢出的高度数结点并将它压入栈
选择：弹出整个栈并指派颜色